Data Envelopment Analysis

Zusammenfassung

Die Data Envelopment Analysis (DEA) bietet Unternehmen im Rahmen des Performance Measurement die Möglichkeit Leistungsprozesse im Hinblick auf die Effizienz messen und beurteilen zu können. Das Verfahren der DEA ermöglicht eine systematische Effizienzmessung in Bereichen, in denen mehrere Inputs und Outputs vorliegen bzw. in den Bereichen in denen keine Gewichtung der einzelnen Input- und Outputfaktoren erfolgen kann. Eine mangelnde Gewichtung der Faktoren liegt in Unternehmen insbesondere in den indirekten Bereichen vor, da der Output nicht am Markt gehandelt wird. Die DEA bietet hier einen Ansatz um die Effizienz insbesondere in indirekten Bereichen der Unternehmen zu messen. Da dabei stets ein Vergleich von Untersuchungsobjekten miteinander erfolgt, ist die DEA als Benchmarking-Instrument charakterisierbar.

Begriffliche Grundlage und Einordnung in das Controlling

Die Data Envelopment Analysis liefert als nicht-parametrische, deskriptive Methodik eine umfangreiche Modellfamilie, die zur Messung der relativen Effizienz bestimmter Untersuchungsobjekte sogenannter Decision Making Units (DMU) oder Entscheidungseinheiten (EE) beiträgt. Eine Entscheidungseinheit kann jedes Objekt sein, das durch Inputs (z.B. Kosten, Arbeitsaufwand in Stunden) und Outputs (bspw. Umsatz, Anzahl Publikationen) charakterisiert werden kann. Diese verschiedenen Faktoren werden mit Hilfe der DEA auf Effizienz untersucht. Im Rahmen der DEA-Anwendung wird für jede Unit ein Optimierungsproblem gelöst an Ende dessen eine Effizienzkennzahl steht. Diese kann auf der einen Seite zur Ermittlung von ineffizienten Einheiten im Rahmen eines Benchmarking genutzt werden.

Methode der Leistungsmessung

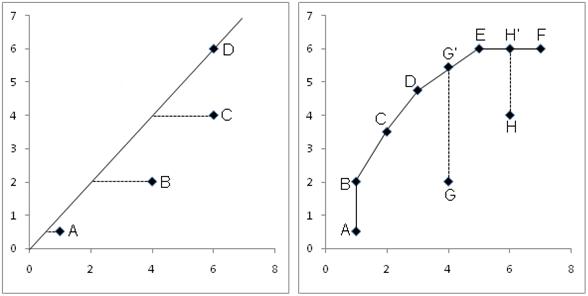
Die Ausprägungen der DEA-Modellfamilie haben alle gemeinsam, dass das vorgeschlagene Maß der Leistungsfähigkeit (Effizienzmaß) jeder möglichen DMU als das Maximum des Verhältnisses der gewichteten Outputfaktoren zu den gewichteten Inputfaktoren verstanden wird. Der so gebildete Quotient wird in einem eigenen Optimierungsvorgang für jede einzelne DMU gelöst. Wobei die Gewichtungen der verschiedenen Faktoren nicht willkürlich gewählt werden, sondern einen realen Gegenstand der Optimierung darstellen. Es werden bei den unterschiedlichen Modellansätzen verschiedene Voraussetzungen impliziert. Im Bereich der Skalenerträge wird zwischen variablen und konstanten Erträgen und im Bereich der Orientierung der Anpassung zwischen inputorientiert, outputorientiert und additiven Ausprägungen unterschieden. Im Rahmen der Anpassung werden die In- und Outputfaktoren der ineffizienten Einheiten variiert, bis die Effizienzkurve erreicht ist. Innerhalb einer vergleichenden Gruppe werden die besten bzw. die beste Einheit als „Best-in-Class“ bezeichnet und gilt als effizient. Diese Einheiten dominieren alle weiteren DMUs, die wiederum als ineffizient bezeichnet werden. Die Dominanz beschreibt in diesem Fall, dass es keine Einheit mit gleichem Output und geringerem Input bzw. keine Einheit mit gleichem Input und höherem Output gibt, was der Voraussetzung von Effizienz entspricht. Die besten Einheiten stellen grafisch gesehen eine Funktion dar, die alle ineffizienten Einheiten einschließt bzw. umhüllt und daher auch als Umhüllende bezeichnet wird. Das Konzept der Skalenerträge bezieht sich auf den effizienten Rand, auf dem eine Vergleichseinheit liegt bzw. auf den eine ineffiziente Einheit projiziert wird. Bei konstanten Skalenerträgen bildet wie in Abbildung 1 zu sehen ist eine Gerade durch den Ursprung und die beste Einheit die Effizienzhülle. Im Fall von variablen Skalenerträgen (Abbildung 1), bilden die verschiedenen „Best-in-Class- Einheiten“ eine „Best-in-Class-Produktionsfunktion“. Diese wird in der Literatur auch als „best-practice frontier“, „Effizienzhülle“, „Envelopment Form“ oder auch „Effizienzrand“ bezeichnet. Abschließend wird für jede nicht effiziente DMU der Grad ihrer Ineffizienz berechnet, dieser entspricht genau dem maximalen Abstand zur effizienten Envelopment Form.

Abb. 1: Effizienzhülle bei konstanten Skalenerträgen (links) und variablen Skalenerträgen (rechts)

Grundlegende Anwendungsbereiche und Prämissen der DEA

Das originäre Einsatzfeld der DEA ist der „Non-Profit“ Sektor, da hier keine monetären Erfolge ausgewiesen werden. Daraus ergibt sich ein Gewichtungsproblem für die ver-wendeten In- und Outputfaktoren. Welches Potenzial dieses Verfahren in sich birgt, zeigt die schnelle Verbreitung. Im Laufe der Zeit fanden auch in privatwirtschaftlichen Unternehmungen wie Kreditinstituten oder Industriebetrieben Untersuchungen mit Hilfe der DEA statt, da in vielen Bereichen eine monetäre Größe in der Regel keine eindeutige Aussage über die Qualität von Unternehmensbereichen erlaubt. Genau diese Forderung nach einem Instrument für die Effizienzmessung der Mehrdimensionalität der Leistungserbringung erfüllt die DEA. Grundlegende Voraussetzung für die DEA-Nutzer ist die Festlegung der Out- und Inputarten in Bezug auf Messbarkeit und Vollständigkeit, d. h. sie müssen alle relevanten Aspekte, die die Effizienz einer DMU prägen, erfassen. Des Weiteren müssen die verschiedenen DMUs homogen, also untereinander vergleichbar und einfach im Sinne von nicht zu detailliert sein.

In Anlehnung an diese Anforderungen lassen sich diese und weitere Prämissen ableiten und sind in Abbildung 2 zu finden.

Abb. 2: Effizienzhülle bei konstanten Skalenerträgen (links) und variablen Skalenerträgen (rechts)

Stärken und Schwächen der DEA

Zu den Stärken der DEA zählt im Vergleich zu den parametrischen Verfahren, dass die Gewichtung der berücksichtigten Inputs und Outputs nicht a-priori festgelegt wird, und somit auf der einen Seite die Gefahr der systematischen Verzerrung verringert wird. Ein weiterer Vorteil ist, dass die DEA effiziente DMUs von den ineffizienten separiert und es keiner subjektiven Einschätzung Außenstehender bedarf, um eine mögliche Produktionsfunktion zu bestimmen. Für jede betrachtete DMU wird eine eigene individuelle Optimierung vollzogen und nicht, wie bei anderen Messverfahren, nur ein Durchschnittswert gebildet. Des Weiteren ist die DEA in der Lage, der Kritik an vielen traditionellen Effizienzmaßen, denen ein reiner Vergangenheitsbezug vorgeworfen wird, entgegenzuwirken, da als Alternative zum Vergleich über die Zeit eine Gegenüberstellung mit den Einheiten innerhalb einer homogenen Gruppe angestrebt werden kann. Ferner identifiziert die DEA individuelle Benchmarking-Partner für die ineffizienten DMUs und schafft dadurch für diese Transparenz, welche Anstrengungen mit Blick auf die untersuchten Inputs und Outputs zu unternehmen sind, um effizient zu werden.

Eine Schwäche der DEA liegt in der Beurteilung der relativen Effizienz von Entschei-dungseinheiten im Gegensatz zur absoluten Effizienz. Daher bleibt die Frage offen, inwieweit eine Vergleichseinheit tatsächlich effizient ist. Diese Kritik wird dadurch abgeschwächt, dass für eine Behebung dieses Nachteils die Technik, unter der alle Einheiten operieren, bekannt sein müsste und dies hätte zur Folge, dass ein Einsatz der DEA überflüssig wäre. Problematisch bei der Data Envelopment Analysis ist, dass es sich um ein deterministisches Verfahren handelt und somit Messfehler in betrachteten Entscheidungseinheiten nicht systematisch in Form einer Verteilungsannahme ausgeschlossen werden können. Zudem ist bei der Anwendung der DEA darauf zu achten, dass keine potenziell relevanten Variablen ausgelassen werden.

Quellen

Charnes, A., Cooper, W.W., Lewin, A.Y., Seiford, L.M. (1994), Data Envelopment Analysis: Theroy, Methodology, and Application, Bosten 1994

Cooper, W.W., Seiford, L.M., Tone,K. (2006), Introduction to Data Envelopment Analy-sis and is uses (With DEA-Solver Software and References), New York 2006

Cooper, W.W., Seiford, L.M., Zhu, J. (2004), Handbook of Data Envelopment Analysis, Bosten 2004

Ahn, H. (2014), Data Envelopment Analysis - Mehr als Benchmarking, in: Controller Magazin, 39. Jg., H. 5, S. 63–65.

Kleine, A. (2002), DEA-Effizienz: Entscheidungs- und produktionstheoretische Grundlagen der Data Envelopment Analysis, Wiesbaden 2002

Schefczyk, M. (1996), Data Envelopment Analysis. Eine Methode zur Effizienz- und Erfolgsschätzung von Unternehmen und öffentlichen Organisationen, in: Die Betriebs-wirtschaft, 56. Jg. (1996), H. 2, S. 167-183

Ersteinstellender Autor

Prof. Dr. Klaus Möller

Kontaktadresse: Klaus.Moeller@unisg.ch

Homepage: [1] - www.aca.unisg.ch