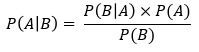Bayes-Theorem

Mit Hilfe des so genannten Bayes-Theorems lassen sich unbekannte Parameter einer Wahrscheinlichkeitsverteilung schätzen, Konfidenzintervalle für die unbekannten Parameter festlegen und Hypothesen über die Parameter prüfen. Das Bayes-Theorem betrachtet so genannte „bedingte Wahrscheinlichkeiten“. Durch diese wird der Tatsache Rechnung getragen, dass im Allgemeinen eine Aussage davon abhängt, ob eine weitere Aussage wahr ist. Man schreibt A|B, um auszudrücken, dass A wahr ist unter der Bedingung, dass B wahr ist. Die Wahrscheinlichkeit von A|B, die bedingte Wahrscheinlichkeit, wird mit P(A|B) bezeichnet. Sie ist ein Maß für die Plausibilität oder Glaubwürdigkeit der Aussage A|B.

Grundsätzlich gibt das Bayes-Theorem an, wie die A-priori-Wahrscheinlichkeit einer Hypothese (Annahme) und bedingte Wahrscheinlichkeiten für bereits eingetretene Ereignisse zu kombinieren sind, um die A-posteriori-Wahrscheinlichkeit einer Hypothese zu bestimmen. Die A-priori-Wahrscheinlichkeit stellt dabei die Wahrscheinlichkeitsschätzung (über ein unbekanntes Ereignis) dar, die aufgrund von Vorwissen, z.B. über das „Design“ (Erfahrungen), angenommen wird.

Demgegenüber gibt die A-posteriori-Wahrscheinlichkeit die Wahrscheinlichkeit an, dass eine Hypothese nach bestimmten (neuen) beobachtbaren Ereignissen bestätigt wird. Mathematisch verhält sich die A-posteriori-Wahrscheinlichkeit, also P(A|B), für die Gültigkeit der Hypothese A nach dem Eintritt des Ereignisses B, wie folgt:

Wobei P(A) und P(B) die Wahrscheinlichkeit von A und B angeben.

Literatur

Zhou, S. (2005): Auf dem falschen Dampfer? Anwendung des Bayes-Theorems zur Risiko-Abschätzung in der stra-tegischen Unternehmensplanung, in: RiskNews, 06/2005, S. 71–74

Ersteinstellender Autor

Prof. Dr. Werner Gleißner