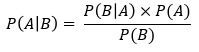Bayes-Theorem: Unterschied zwischen den Versionen
Aus ControllingWiki
Achtung. Sie nutzen eine nicht mehr unterstützte Version des Internet Explorer. Es kann zu Darstellungsfehlern kommen. Bitte ziehen Sie einen Wechsel zu einer neueren Version des Internet Explorer in Erwägung oder wechseln Sie zu einer freien Alternative wie Firefox.| [unmarkierte Version] | [geprüfte Version] |
(Die Seite wurde neu angelegt: „Mit Hilfe des so genannten Bayes-Theorems lassen sich unbekannte Parameter einer Wahrscheinlichkeitsverteilung schätzen, Konfidenzintervalle für die unbekan…“) |
|||
| Zeile 1: | Zeile 1: | ||
| + | ''Prüfsiegel gültig bis 2021'' | ||
| + | |||
Mit Hilfe des so genannten Bayes-Theorems lassen sich unbekannte Parameter einer Wahrscheinlichkeitsverteilung schätzen, Konfidenzintervalle für die unbekannten Parameter festlegen und Hypothesen über die Parameter prüfen. Das Bayes-Theorem betrachtet so genannte „bedingte Wahrscheinlichkeiten“. Durch diese wird der Tatsache Rechnung getragen, dass im Allgemeinen eine Aussage davon abhängt, ob eine weitere Aussage wahr ist. Man schreibt A|B, um auszudrücken, dass A wahr ist unter der Bedingung, dass B wahr ist. Die Wahrscheinlichkeit von A|B, die bedingte Wahrscheinlichkeit, wird mit P(A|B) bezeichnet. Sie ist ein Maß für die Plausibilität oder Glaubwürdigkeit der Aussage A|B. | Mit Hilfe des so genannten Bayes-Theorems lassen sich unbekannte Parameter einer Wahrscheinlichkeitsverteilung schätzen, Konfidenzintervalle für die unbekannten Parameter festlegen und Hypothesen über die Parameter prüfen. Das Bayes-Theorem betrachtet so genannte „bedingte Wahrscheinlichkeiten“. Durch diese wird der Tatsache Rechnung getragen, dass im Allgemeinen eine Aussage davon abhängt, ob eine weitere Aussage wahr ist. Man schreibt A|B, um auszudrücken, dass A wahr ist unter der Bedingung, dass B wahr ist. Die Wahrscheinlichkeit von A|B, die bedingte Wahrscheinlichkeit, wird mit P(A|B) bezeichnet. Sie ist ein Maß für die Plausibilität oder Glaubwürdigkeit der Aussage A|B. | ||
Aktuelle Version vom 27. Januar 2019, 11:11 Uhr
Prüfsiegel gültig bis 2021
Mit Hilfe des so genannten Bayes-Theorems lassen sich unbekannte Parameter einer Wahrscheinlichkeitsverteilung schätzen, Konfidenzintervalle für die unbekannten Parameter festlegen und Hypothesen über die Parameter prüfen. Das Bayes-Theorem betrachtet so genannte „bedingte Wahrscheinlichkeiten“. Durch diese wird der Tatsache Rechnung getragen, dass im Allgemeinen eine Aussage davon abhängt, ob eine weitere Aussage wahr ist. Man schreibt A|B, um auszudrücken, dass A wahr ist unter der Bedingung, dass B wahr ist. Die Wahrscheinlichkeit von A|B, die bedingte Wahrscheinlichkeit, wird mit P(A|B) bezeichnet. Sie ist ein Maß für die Plausibilität oder Glaubwürdigkeit der Aussage A|B.
Grundsätzlich gibt das Bayes-Theorem an, wie die A-priori-Wahrscheinlichkeit einer Hypothese (Annahme) und bedingte Wahrscheinlichkeiten für bereits eingetretene Ereignisse zu kombinieren sind, um die A-posteriori-Wahrscheinlichkeit einer Hypothese zu bestimmen. Die A-priori-Wahrscheinlichkeit stellt dabei die Wahrscheinlichkeitsschätzung (über ein unbekanntes Ereignis) dar, die aufgrund von Vorwissen, z.B. über das „Design“ (Erfahrungen), angenommen wird.
Demgegenüber gibt die A-posteriori-Wahrscheinlichkeit die Wahrscheinlichkeit an, dass eine Hypothese nach bestimmten (neuen) beobachtbaren Ereignissen bestätigt wird. Mathematisch verhält sich die A-posteriori-Wahrscheinlichkeit, also P(A|B), für die Gültigkeit der Hypothese A nach dem Eintritt des Ereignisses B, wie folgt:
Wobei P(A) und P(B) die Wahrscheinlichkeit von A und B angeben.
Literatur
Zhou, S. (2005): Auf dem falschen Dampfer? Anwendung des Bayes-Theorems zur Risiko-Abschätzung in der stra-tegischen Unternehmensplanung, in: RiskNews, 06/2005, S. 71–74
Ersteinstellender Autor
Prof. Dr. Werner Gleißner