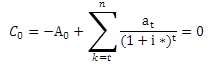Interner Zinsfuß

Prüfsiegel gültig bis 2022

Definition

Der interne Zinsfuß ist derjenige Zins bei dem der Kapitalwert der Investition gleich Null ist. Rechnerisch erhält man den internen Zinsfuß indem man die obere Gleichung nach i* auflöst.

Dabei gilt:

C Kapitalwert, in der Regel wird auf die Periode Null gerechnet

A Anschaffungs-/Investitionsauszahlung(en), auch hier i.d.R. auf Periode Null bezogen

n Gesamte Anzahl der Perioden

t Periode, die an dieser Stelle durch die Formel berechnet wird

i Zinssatz (interest), hier der gesuchte interne Zinsfuß

a Zahlungssaldo (aus Ein- und Auszahlungen) der Periode

Datenbeschaffung

siehe: Kapitalwert

Interpretation

Der Interne Zinsfuß ist derjenige Zinsfuß, bei dem der Kapitalwert der Ein- und Auszahlungsreihen des Investitionsprojektes gleich Null ist. Er ist somit ein kritischer Wert und kann bei einer einzelnen Investition als Entscheidungskriterium für die Durchführung bzw. Unterlassung der Investition herangezogen werden:

1. Falls der Interne Zinsfuß kleiner als die Kapitalkosten ist, ist der Kapitalwert negativ. Die Investition vernichtet Wert und es wäre sinnvoll sie zu unterlassen.
2. Ist der Interne Zinsfuß gleich der Kapitalkosten, ist der Kapitalwert gleich Null. Die Investition erwirtschaftet die Kapitalkosten und kann durchgeführt werden.
3. Falls der Interne Zinsfuß größer als die Kapitalkosten ist, ist der Kapitalwert positiv und somit die Investition 'rentabel', d.h. sie schafft einen ökonomischen Mehrwert.

Hinweise zur Anwendung

Der Interne Zinsfuß kann zur Beurteilung einer Investition - wie oben beschrieben - verwendet werden.

Zwei oder mehrere Investitionsprojekte können im Regelfall nicht anhand der internen Zinsfußmethode miteinander verglichen werden. Der bequeme und schnelle Vergleich zweier Zinsfüße erlaubt ohne weitere, i.d.R. sehr komplizierte Ergänzungsrechnungen, keine Aussage über die relative Vorteilhaftigkeit. Es ist nicht richtig, dass die Investition mit dem höheren Internen Zinsfuß grundsätzlich vorteilhaft ist. Es ist noch nicht einmal so, dass sie meistens vorteilhaft ist.

Der Grund liegt in der nicht direkt erkennbaren Wiederanlageprämisse, die dem internen Zinsfuß bei der Berechnung zugrunde liegt. Sie führt zu teilweise dramatischen inhaltlichen Fehlern. Der Interne Zinsfuß sollte daher allenfalls als ergänzendes Kriterium bei einer Investitionsbeurteilung angewandt werden.

Soll unbedingt mit einem Zins gearbeitet werden, so ist die "modifizierte Interne ZInsfußmethode" (auch Baldwin-Zins) besser geeignet.

Hinweise zur Berechnung

Der interne Zinsfuß ist nicht immer durch Auflösung eines Gleichungssystems eindeutig bestimmbar. Nur für wenige Sonderkonstellationen gibt es eine Formel. Auch mathematische Programme, wie z.B. Excel, finden die Lösung daher durch Iteration, d.h. einen Suchprozess. Nur im Fall einer sogenannten "Normalinvestition" ist sichergestellt, dass es nur einen internen Zinsfuß gibt. Bei allen anderen Investitionen kann es mehrere Interne Zinsfüße geben. Als Interner Zinsfuß kann sich auch ein negativer Prozentwert ergeben.

Literatur

Thomas Biasi, Alfred Blazek, Klaus Eiselmayer: „Finanz-Controlling – Planung und Steuerung von Bilanzen und Finanzen“, 9. Vollständig neu bearbeitete Auflage, Verlag für ControllingWissen AG, Freiburg.

Seminarmappe des Fachseminars "Investitions-Controlling" der CA Controller Akademie AG, Wörthsee, Stand: März 2013.

Ersteinstellender Autor

Guido Kleinhietpaß, [ http://www.controllerakademie.de] fachseminare/investitions-controlling.html
Sebastian Dietzel